CirclePattern Struct Reference

#include <CirclePattern.h>

List of all members.

Detailed Description

Defines functions that compute quantities relevant to circle pattern energy.

EnergyMinimization class calls these functions while solving the non-linear problem.

The most important functions are evaluateEnergy, computeGradient, computeHessian, and buildSparsityForHessian. These functions can be modified to use different non-linear solver and different datastructures for gradient and Hessian.

The energy is computed as:

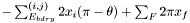
$S_{ecl}(x)=\sum_{E_{int}}^{(i,j)} [ \textrm{ ImLi2Sum }(\theta, x_i - x_j) - (\pi - \theta)(x_i - x_j)]$ $- \sum_{E_{bdry}}^{(i,j)} 2 x_i (\pi-\theta) + \sum_{F}2\pi x_f$

The gradient is:

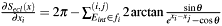
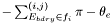
$\frac{\partial S_{ecl}(x)}{\partial x_i} = 2\pi - \sum_{E_{int}\in f_i}^{(i,j)}2 \arctan \frac{\sin\theta}{e^{x_i-x_j} - \cos\theta}$ $- \sum_{E_{bdry} \in f_i}^{(i,j)} \pi-\theta_e$

The Hessian is:

$\frac{\partial^2 S_{ecl}(x)}{\partial x_i \partial x_j} = -\frac {\sin(\theta)}{\cosh(x_i-x_j) - \cos(\theta)}$

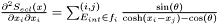
$\frac{\partial^2 S_{ecl}(x)}{\partial x_i \partial x_i} = \sum_{E_{int}\in f_i}^{(i,j)} \frac {\sin(\theta)}{\cosh(x_i-x_j) - \cos(\theta)}$

All the sums are taken over edges (not the half-edges). The variables x represent logarithm of the radii of the triangles in the mesh. The variables 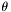$\theta$ are defined for each edge and represent an angle of intersection of two circumcircles of triangles meeting on this edge.

Definition at line 43 of file CirclePattern.h.

Static Public Member Functions

static double evaluateEnergy (Mesh *mesh, double *xx)
 Computes circle pattern energy for the mesh.
static void computeGradient (Mesh *mesh, double *xx, double *grad)
 Computes gradient vector for circle pattern energy.
static void buildSparsityForHessian (Mesh *mesh, int *hessI, int *hessJ)
 Sets the sparsity pattern of the non-zeros in the Hessian.
static void computeHessian (Mesh *mesh, double *xx, double *hessval)
 Computes the sparse Hessian of circle pattern energy.
static double ImLi2Sum (const double &theta, const double &x, const double &tanHalfThetaStar, const double &clThetaStar)
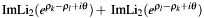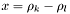 Computes $\textrm{ ImLi}_2(e^{\rho_k - \rho_l+i\theta}) + \textrm{ ImLi}_2(e^{\rho_l - \rho_k+i\theta})$ , where $x=\rho_k - \rho_l$ .
static double Cl2 (const double &_x)
 Implementation of Clausen integral taken from Boris Springborn's code.
static double fTheta2 (const double &cosTheta, const double &sinTheta, const double &x)
 Computes 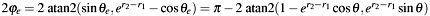$2\varphi_e=2\textrm{ atan2}(\sin\theta_e, e^{r_2-r_1} - \cos\theta_e)=\pi-2\textrm{ atan2}(1-e^{r_2-r_1}\cos\theta, e^{r_2-r_1}\sin\theta)$.
static double fThetaPrime2 (const double &cosTheta, const double &sinTheta, const double &x)
 Computes 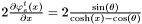$2\frac{\partial \varphi_e^t(x)}{\partial x} = 2\frac {\sin(\theta)}{\cosh(x) - \cos(\theta)}$.
static double IEEEremainder (const double &x, const double &div)
 Reimplementation of java version of IEEEremainder, when x is divided by div.

Member Function Documentation

void CirclePattern::buildSparsityForHessian (  Mesh *  mesh,
int *  hessI,
int *  hessJ
)  [static]
 

Sets the sparsity pattern of the non-zeros in the Hessian.

Non-zeros on the diagonal

And non zero element [i][j] for each internal edge (i,j)

Definition at line 110 of file CirclePattern.cpp.

00110                                                                                   {
00111    int i, k, j;
00112 
00114    for (k = 0; k < mesh->numFaces(); k++) {
00115       hessI[k] = k; 
00116       hessJ[k] = k;
00117    }
00118 
00119    k = mesh->numFaces();
00121    Mesh::HalfEdgeIterator hIter = mesh->halfEdgeIterator();
00122    for (hIter.reset(); !hIter.end(); hIter++) {
00123       if (!hIter.half_edge()->isBoundary()) {
00124           i = hIter.half_edge()->face->ID;
00125           j  = hIter.half_edge()->pair->face->ID;
00126           if (i > j) {
00127              hessI[k] = i; 
00128              hessJ[k] = j;
00129              k++;
00130           }       
00131       }
00132    }
00133 }

double CirclePattern::Cl2 (  const double &  _x  )  [inline, static]
 

Implementation of Clausen integral taken from Boris Springborn's code.

Definition at line 105 of file CirclePattern.h.

00105                                                    {
00106    double TWO_PI = 2 * M_PI;
00107    double MINUS_LOG_2 = log(0.5);
00108    double BORDERLINE = 2.0944;
00109 
00110    if (_x == 0.0) {
00111       return 0.0;
00112    }
00113 
00114    double x = IEEEremainder(_x, TWO_PI);
00115 
00116    if (x == 0.0) {
00117       return 0.0;
00118    }
00119 
00120    if (fabs(x) <= BORDERLINE) {
00121       double xx = x * x;
00122       return ((((((((((((
00123           2.3257441143020875e-22 * xx
00124           + 1.0887357368300848e-20) * xx 
00125           + 5.178258806090624e-19) * xx
00126           + 2.5105444608999545e-17) * xx
00127           + 1.2462059912950672e-15) * xx
00128           + 6.372636443183181e-14) * xx
00129           + 3.387301370953521e-12) * xx
00130           + 1.8978869988971e-10) * xx
00131           + 1.1482216343327455e-8) * xx
00132           + 7.873519778281683e-7) * xx
00133           + 0.00006944444444444444) * xx
00134           + 0.013888888888888888) * xx 
00135           - log(fabs(x)) + 1.0) * x;
00136    }
00137    x += ((x > 0.0) ? - M_PI : M_PI);
00138    double xx = x * x;
00139    return ((((((((((((  
00140       3.901950904063069e-15 * xx
00141       + 4.566487567193635e-14) * xx
00142       + 5.429792727596476e-13) * xx
00143       + 6.5812165661369675e-12) * xx
00144       + 8.167010963952222e-11) * xx
00145       + 1.0440290284867003e-9) * xx
00146       + 1.3870999114054669e-8) * xx
00147       + 1.941538399871733e-7) * xx
00148       + 2.927965167548501e-6) * xx
00149       + 0.0000496031746031746) * xx
00150       + 0.0010416666666666667) * xx
00151       + 0.041666666666666664) * xx 
00152       + MINUS_LOG_2) * x;
00153 }

void CirclePattern::computeGradient (  Mesh *  mesh,
double *  xx,
double *  grad
)  [static]
 

Computes gradient vector for circle pattern energy.

For each triangle t: $\textrm{ Grad}(t) = 2\pi - \sum_{e \in t}2\varphi_e^t$ ,

where for internal edge e: $\varphi_e^t=\frac{\pi}{2}-\textrm{ atan2}(1 - e^x \cos\theta_e ,e^x \sin\theta_e)$ , with $x = xx_i - xx_j$ ; and for boundary edge e: $\varphi_e^t=\pi-\theta_e$ .

Definition at line 80 of file CirclePattern.cpp.

00080                                                                             {
00081 
00082    Mesh::FaceIterator fIter = mesh->faceIterator();
00083 
00084    /* Compute and store the gradient of the f. */
00085    int i, j;
00086    for (i = 0; i < mesh->numFaces(); i++)
00087       grad[i] = M2_PI;
00088 
00089    // sum over edges
00090    Mesh::HalfEdgeIterator hIter = mesh->halfEdgeIterator();
00091    for (hIter.reset(); !hIter.end(); hIter++) {
00092       Edge * e = hIter.half_edge();
00093       if (!e->isBoundary()) {
00094           i = e->face->ID;
00095           j = e->pair->face->ID;
00096           if (i > j) {
00097              grad[i] -= fTheta2(e->cosTheta(), e->sinTheta(), xx[j] - xx[i]);
00098              grad[j] -= fTheta2(e->cosTheta(), e->sinTheta(), xx[i] - xx[j]);
00099           }
00100       }
00101       else if (e->face) {
00102           i = e->face->ID;
00103           grad[i] -= 2*(M_PI - e->theta());
00104       }
00105    }
00106 
00107 }

void CirclePattern::computeHessian (  Mesh *  mesh,
double *  xx,
double *  hessval
)  [static]
 

Computes the sparse Hessian of circle pattern energy.

The value of Hessian[i][j] = Hessian [j,i] = -$\frac{\partial \varphi_e^t(x)}{\partial x} = -\frac {\sin(\theta)}{\cosh(x) - \cos(\theta)}$ ; The value of Hessian[i][i] = $\sum_{e \in t_i} \frac{\partial \varphi_e^t(x)}{\partial x}$ , with $x = xx_i - xx_j$ .

Definition at line 142 of file CirclePattern.cpp.

00142                                                                               {
00143    for (int k = 0; k < mesh->numFaces(); k++) 
00144       hessval[k] = 0;
00145 
00146    int count = mesh->numFaces();
00147    int i,j;
00148    Mesh::HalfEdgeIterator hIter = mesh->halfEdgeIterator();
00149    for (hIter.reset(); !hIter.end(); hIter++) {
00150       Edge * e = hIter.half_edge();
00151       if (!e->isBoundary()) {
00152           i = e->face->ID;
00153           j = e->pair->face->ID;
00154           if (i > j) {
00155              double ximj = xx[i] - xx[j];
00156              double fThPrime2 = fThetaPrime2(e->cosTheta(), e->sinTheta(), ximj);
00157              hessval[count] = -fThPrime2;
00158              hessval[i] += fThPrime2;
00159              hessval[j] += fThPrime2;
00160              count++;
00161           }
00162       }
00163    }
00164 }

double CirclePattern::evaluateEnergy (  Mesh *  mesh,
double *  xx
)  [static]
 

Computes circle pattern energy for the mesh.

The energy is computed as: $\sum_{E_{int}} (ImLi2Sum(\theta, x_i - x_j) - (\pi - \theta)(x_i - x_j)) - \sum_{E_{bdry}} 2 x_i (\pi-\theta) + \sum_{F}2\pi x_f$

Definition at line 40 of file CirclePattern.cpp.

00040                                                              {
00041    int i, j;
00042    double energy = 0;
00043    for (i = 0; i < mesh->numFaces(); i++) {
00044       energy += xx[i];
00045    }
00046 
00047    energy = M2_PI*energy;   // Total contribution from faces
00048 
00049    Mesh::HalfEdgeIterator hIter = mesh->halfEdgeIterator();
00050    for (hIter.reset(); !hIter.end(); hIter++) {
00051       Edge * e = hIter.half_edge();
00052 
00053       if (!e->isBoundary()) {
00054           i = e->face->ID;
00055           j = e->pair->face->ID;
00056           if (i > j) {
00057              double theta = e->theta();
00058              energy += ImLi2Sum(theta, xx[i] - xx[j], e->tanHalfTStar(), e->Cl2TStar());
00059              energy -= (M_PI - theta)*(xx[i] + xx[j]);
00060           }
00061       }
00062       else {
00063           if (e->face) {
00064              i = e->face->ID;
00065              energy -= 2*(M_PI - e->theta())*(xx[i]);
00066           }
00067       }
00068    }
00069    return energy;
00070 }

double CirclePattern::fTheta2 (  const double &  cosTheta,
const double &  sinTheta,
const double &  x
)  [inline, static]
 

Computes $2\varphi_e=2\textrm{ atan2}(\sin\theta_e, e^{r_2-r_1} - \cos\theta_e)=\pi-2\textrm{ atan2}(1-e^{r_2-r_1}\cos\theta, e^{r_2-r_1}\sin\theta)$.

Definition at line 74 of file CirclePattern.h.

00074                                                                                                    {
00075    double ex = exp(x);
00076    double s1 = 1.0 - ex*cosTheta;
00077    double s2 = ex*sinTheta;
00078 
00079    double res = M_PI - 2*atan2(s1, s2);
00080 
00081    return res;
00082 }

static double CirclePattern::fThetaPrime2 (  const double &  cosTheta,
const double &  sinTheta,
const double &  x
)  [inline, static]
 

Computes $2\frac{\partial \varphi_e^t(x)}{\partial x} = 2\frac {\sin(\theta)}{\cosh(x) - \cos(\theta)}$.

Definition at line 65 of file CirclePattern.h.

00065                                                                                                  {
00066       double res = sinTheta/(cosh(x) - cosTheta);
00067       return res;
00068    }

double CirclePattern::IEEEremainder (  const double &  x,
const double &  div
)  [inline, static]
 

Reimplementation of java version of IEEEremainder, when x is divided by div.

Definition at line 84 of file CirclePattern.h.

00084                                                                                {
00085 
00086    double  res;
00087    if (x >= 0) {
00088       if (x < div) res = x;
00089       else {
00090           double part = floor(x / div);
00091           res = x - part*div;
00092       }
00093    }
00094    else {
00095       double part = floor(x / div);
00096       res = x - part*div;
00097    }
00098    if (res < 0 || res > div) {
00099       std::cout << "x " << x << " div " << div << std::endl;   
00100       std::cerr << "Wrong IEEEreminder!!!" << std::endl;
00101    }
00102    return res;
00103 }

double CirclePattern::ImLi2Sum (  const double &  theta,
const double &  x,
const double &  tanHalfThetaStar,
const double &  clThetaStar
)  [static]
 

Computes $\textrm{ ImLi}_2(e^{\rho_k - \rho_l+i\theta}) + \textrm{ ImLi}_2(e^{\rho_l - \rho_k+i\theta})$ , where $x=\rho_k - \rho_l$ .

Parameters:
theta valid theta angle for edge e
x $=\rho_k - \rho_l=\log(r_k) - \log(r_l)$
tanHalfThetaStar $=\tan(\frac{\pi - \theta}{2})$
clThetaStar $=\textrm{Cl}_2(2(\pi - \theta))$ .

Definition at line 23 of file CirclePattern.cpp.

00025 {
00026    double tStar = M_PI - theta;
00027    double p = 2*atan(tanh(0.5*x)*tanHalfThetaStar);
00028 
00029    return  p*x + Cl2(p + tStar) + Cl2(-p + tStar) - clThetaStar;
00030 }

The documentation for this struct was generated from the following files:
Generated on Sat Jun 3 13:33:42 2006 for CirclePatterns by  doxygen 1.4.5